スタッフの日記

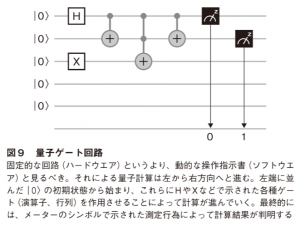
５．そもそも量子コンピュータって、何だっけ
　その後、何冊か読んだが、今回は、

　　　「スッキリ！がってん！　量子コンピュータの本（森 貴洋、ISBN978-4-485-60043-6）」

を読んで、知識を深めたことを中心に述べたいと思う。
　この本では、「量子コンピュータの基礎」を、「今のコンピュータ」から説き起こしている。
　そして、「量子ってなあに」との問いに答える形で、基礎の基礎を説いている。
　そこでは、「量子」の「子」についての説明もある。

　しかし、なぜ〝量〟子なのかの問いには答えていない。
　筆者は、その説明が、以前に読んだ本にあったのを思い出し、その本

　　　「りょうしりきがく for babies （作：クリス・フェリー/監訳者：村山　斉、ISBN978-4-7631-3766-1）」

を再度読みなおしてみた。

５．１　そもそも量子って、何だっけ
　「りょうしりきがく for babies」は、一冊丸々が、量子（りょうし、quantum）って、何だっけの説明である。
　要約すると、

　　　● 物質は原子から構成される。
　　　● 原子の中では中性子と陽子が核となり、その周りを電子が走りまわっている。
　　　● 電子が走り回る複数の「レール」があって、電子はどれかのレール上にある。
　　　● 核から遠いレールほど、電子のエネルギーが大きい
　　　● 電子がエネルギーをもらうと、遠いレールに飛び上がる。
　　　● 電子がエネルギーを失うと、近いレールに落っこちる。
　　　● この、もらうエネルギー、失うエネルギーの量は、レール対が決まれば確定する。
　　　● この、確定したエネルギー量のことを、「量子」と言う。

となる。
　ここでは、「量子」の実体が何であるかは分からない。
　また、原子とか電子とかが量子なのか否かも分からない。

　この本（りょうしりきがく for babies）の解説とネット情報などによると、上記の内容（前期量子論）は、1905年頃までのことで、その後、「なぜ電子はレールを外れないか」などについての理論の発展があり、「量子力学」として結実した。
　量子力学の特徴は、「量子は『波』である」ということである。
　「波」と聞くと、名画「神奈川沖浪裏」みたいなダイナミックな波を想像したくなるかもしれないが、ちょっと（かなり？）違う。何も波のようには動いてはいないが、「周波数」、「波長」、「位相（phase：topologyとは無関係）」と言うべきものがそれぞれあり、「重ね合わせ」ということができる点などが波と同じなので、「波」という言葉を使っている。

　「量子ってなあに」が一応分かったので、先に進む。
　「量子コンピュータ関連書籍を読んで（その１、その２）」において、「量子を使っているから量子コンピュータと言う訳ではない」ということを述べたが、「スッキリ！がってん！　量子コンピュータの本」でも、そう述べている。
　そして、「『量子』は今のコンピュータをつくるうえでも重要なのだが、『データ』には『量子』を使っていない。『データ』に『量子』を使ったコンピュータ、それが量子コンピュータだ。」と述べている。
　では、「『データ』に『量子』を使う」とは、どういう意味だろうか。

５．２　量子コンピュータでのデータ
　ここに書くことは、どこかの書物とかに書かれているものとは限らない。筆者が諸文献を読んで、理解した内容である。

５．２．１　「0」と「1」
　まずは、コンピュータのデータの基本、「0」と「1」。

　「りょうしりきがく for babies」において「レール上にある」と描かれていたことを拡張して、「状態」という言葉を使用することにする。重ね合わせがある状態は「重ね合わせ状態」、重ね合わせが無い状態は「純粋状態」と呼ぶ。
　「りょうしりきがく for babies」においては、レールは３本あったので、「原子核と１電子の組」の純粋状態は３つ、「レール対に対応したエネルギー」の純粋状態も３つある。
　このように、２つ以上の純粋状態があるとき、そのうちの１つをどれでもよいので決めて「|0>」と名づける。これは、今のコンピュータにおける「0」あるいは「false」に相当する。「スッキリ！がってん！」では「上向き矢印」とも言っている。
　さらに、|0>以外の純粋状態の１つをどれでもよいので決めて「|1>」と名づける。これは「1」あるいは「true」に相当する。「スッキリ！がってん！」では「下向き矢印」。
　「『どれでもよいので』って、そんないい加減なことで良いのか？。」と言われそうだが、筆者の理解では、良いのである。
　今のコンピュータでも、何を「0」とし、何を「1」とするかは、かなりいい加減だと思う。
　なお、「<…|」、「|…>」は、ブラ-ケット記法と呼ばれるもので、「<…|」をブラ、「|…>」をケットと読む。両方で「ブラケット」となる訳である。これらは、量子力学を記述するのに便利な記法として作られたが、量子コンピュータの理論においては、ケットのみを使用し、ブラは使用しない。

　さて、「上向き矢印」と「下向き矢印」があるなら、「右向き矢印」とか「斜め上向き矢印」があっても良い。「スッキリ！がってん！」には、そう言う意味のことが書かれている。
　実は、筆者は当初、「矢印」とあるのは「ベクトル」のことだろうと思って読んでいた。ベクトルとは、「大きさ」と「向き」を持つ量で、「平行四辺形の法則」によって、足し算（合成）と、足し算の逆演算である引き算が定義できるものであると認識している。
　しかし、「スッキリ！がってん！」に書かれた内容は、平行四辺形の法則とは似ても似つかない。
　「反対の向きを向いた矢印は、重なればなくなってしまう。」との記述があるが、これは明らかにウソである。
　たとえば、上向き（|0>）と下向き（|1>）は、反対の向きを向いているが、重ねても無くならない。
　その説明の中に「ブロッホ球」という言葉があったので、ネットを検索してみた。そして、「どうもこれは、私の知っている『ベクトル』ではないらしい。『矢印』という言葉はスッキリしない。」と考えるようになった。
　さらに、「この『矢印』を『ブロッホ・ベクトル』と呼ぶ人もいるらしいが、合点できない。」と思う。

５．２．２　「0」、「1」以外のデータを球面上の点として追加
　では、「矢印」、「ベクトル」でなく、なんという言葉を使ったらスッキリし、合点できるのだろうか。

　筆者は、「時計の針」、「計器の針」の「針(hand)」が良いと思う（「針」という言葉は、誰も使ってないようだ）。
　時計の針なら、|0>は「上向き」なので12時を指し、|1>は「下向き」なので6時を指す。「右向き」は3時、「左向き」は9時。
　しかし、「前向き」とか、「後ろ向き」とかもあるので、時計の針が指せるところ（＝円周上）だけでは足りない。
　それで全体としては球になるので、「ブロッホ〝球〟」。「ブロッホ」は、これを考えた人の名前らしい。

「スッキリ！がってん！量子コンピュータの本」の図2.7より

　球面になるので、地球における緯度、経度に相当するものを考えることもできる。

　但し、緯度に相当するものは、赤道からの角度ではなく、北極（＝|0>）からの角度を用いる。
　だから、北極点は90度でなく0度、赤道上の点は0度でなく90度、南極点は90度でなく180度である。
　北緯なのか、南緯なのかを考える必要は無いし、欧米人が不得手なマイナスの数を考える必要もない。

　また、経度に相当するものは、東経のみを用い、西経は用いない。
　日付変更線を越えても日付は変わらず、180度以上となり、さらに進んでいって、360度に達する。そこでやっと日付が変わる。
　東経なのか、西経なのかを考える必要は無いし、欧米人が不得手なマイナスの数を考える必要もない。
　経度は、位相を表すということになるようだ。

５．２．３　ブロッホ球面上の点に対する演算
　こんなに素晴らしいデータ表現ができても、実際にこれを使って計算ができなければ、意味がない。

　「『どれでもよいので』って、そんないい加減なことで良いのか？。」と上述したが、ブロッホ球面を作るにはそれでよいが、実際に計算に使用することができるためには、やはり、条件がある。
　どうも、ブロッホ球面上からブロッホ球面上への移動は、ブロッホ球面の中心を通る直線を軸として回転するということになる必要があるらしい。
　例えば、９時と３時を結ぶ直線を軸として回転すると、|0>と、|1>は、入れ替わる。これは、NOT演算に似ているが、前向きと後ろ向きが入れ替わるので、NOTとは、ちょっと違う。
　

　「● 電子がエネルギーをもらうと、遠いレールに飛び上がる。」は、「|0>→|1>」だから、ブロッホ球面上での移動だけど、…
　これは、「すべてを|1>にする」という演算になるように思えるが、「位相」を考えると、それはあり得ないらしい。
　

　　　「『量子コンピュータ』超並列計算のからくり（竹内　繁樹、ISBN978-4-06-257469-3）」

を読んで、筆者の拙い頭で考えたのは、
　遠いレールに飛び上がった電子は、すぐにエネルギーを放出して、元のレールに戻る。
　元のレールには、はじめからあった電子と、戻ってきた電子とが「混在」する。
　結果として、はじめからあった電子とは、異なった位相となる。
ということである。

１．電卓型とそろばん型
　量子コンピュータに関する文献を読んで、もしかして、情報処理システムには「電卓型」と「そろ ばん型」があるのではなかろうかと思うようになった。
　電卓型は、たとえば下図。

　「ここから上は出力」、「ここから下は入力」で示したように、入力場所と出力場所とが、きっちり と分かれている。

　人間の脳の細胞（ニューロン）も電卓型。入力場所と出力場所は分かれている（下図）。

　「そろばん型」は、適切な画像が無いが、要するに、入力と出力が分かれていない。

上図は、筆者が小学生の時に買ってもらったもの。

　そして、古典コンピュータ（従来のコンピュータ、現在のコンピュータ）は概ね電卓型、量子コン ピュータは必ずそろばん型となるらしい。

　それは、量子コンピュータが、「波の重ね合わせ」を計算するものだからだと思われる。
　例えば、少量の放射性物質と、それが放射性崩壊したときにそれを検知する検知器と、検知器に連動して瓶を叩き割るハンマーとを箱に入れて蓋をする。放射性崩壊は量子現象なので、ふたを開ける前は、瓶が「割れている状態」と「割れていない状態」との、波としての重ね合わせになっている。
蓋を取らなければ、割れているのか割れていないのか決まらない。蓋を取って箱の中の情報を外部に出力すると、割れているか否かが確定してしまう。つまり「割れていない」と「割れている」の両方があったものが、一方だけになってしまう。
　「量子コンピュータは、このような箱をたくさん並べたようなもの」という意味のことが、「でたらめの科学　サイコロから量子コンピューターまで（ISBN：978-4-02-295104-5）」に書かれている。なので、計算の途中で「波の重ね合わせ」でなくなってしまい、瓶が割れているか否かが確定しては、まずいのである。

　「ゼロからわかる量子コンピュータ（ISBN：978-4-06-528299-1）」に、下図がある。

　この図で水平線は同一の〝もの〟である。〝もの〟としては一つであるが、〝状態〟は、複数の状態の重ね合わせである。
　量子コンピュータのプログラミングは、上図の、、、などの「ゲート」を、どこに配置するかを考えることになる訳である。
　量子コンピュータにおける「ゲート」は、「偏光を当てる」とか「磁場をかける」などの操作である。そろばんにおける、指の動かし方に相当するものだと思う。
　そして、ややこしいことに、「一番上の瓶が割れていない状態と、二番目の瓶が割れている状態の重ね 合わせ」などというのもありうる。上図で縦につながった「ゲート」は、このような、複数の瓶の状態の 重ね合わせに対する操作であろう。
　ということは、古典コンピュータのプログラムが、基本的に１次元であるのに対し、量子コンピュー タのプログラムは、ほとんどの場合、２次元以上となるのではなかろうか。
　ちなみに、は、状態を表現するもので、左側に縦線、右側に閉じ括弧（〉）を書く。

余談：
　テレビの時代劇を見ていたら、五珠が２つ、一珠が５つのそろばんが使われていました。
　ネットを検索すると、「もともと１３世紀ころ中国で発明された算盤は、重量の単位で１斤＝１６両、面積の単位で1市頃=１６市畝など、１６進数が計算できるように、五珠が２つ、一珠が５つだった。」ということのようです。

２．量子を使っているから量子コンピュータと言う訳ではないということ
　今日使われている、いわゆるノイマン型コンピュータは、「電子計算機」とも呼ばれている。「電気 計算機」とか「電動計算機」とか言うと、別のものになってしまう。つまり、電気を使用していることが 本質なのではなく、電子を使用していることが本質なのである。
　そして、電子は、量子の一種である。
　今日のコンピュータには、半導体が使われている。半導体にはｎ型半導体とｐ型半導体があって、それらの薄片を何層にも貼り合わせたものを使う。
　そして、電流は、ｐ型半導体からｎ型半導体へは流れるが、ｎ型半導体からｐ型半導体へは流れ ない。
しかし、そのｎ型半導体のところにもう一つｐ型半導体をくっつけて、そのｐ型半導体からｎ型半導体に電流を流すと、流れなかったｎ型半導体からｐ型半導体への電流が流れる。
　この不思議な現象は、量子論によらなければ説明できない。そもそも、なぜｎ型半導体とｐ型半導体とが存在するのかが、量子論によらなければ説明できない。
　今日のコンピュータは、これらの量子現象を演算処理等に使っている。
　量子を使っているにもかかわらず、今日普通に使われているパソコンやスーパー・コンピュータ は、量子コンピュータではない。
　たとえば、「量子コンピュータの衝撃(ISBN：978-4-299-00338-6)」には、「古典コンピュータは電 子を使っているのに、何故量子コンピュータと呼ばないのか」という疑問が表明され、それなりの回 答を示している。しかし、「粒子の数が多くなると波のように見える」などと的外れなことを言ってい る。
　筆者は、この回答も含めた諸々の考察の末、「電子を個別処理するのが量子コンピュータ、 電子を集団で処理するのが古典コンピュータ」という結論に達した。

【参考にした文献】（量子コンピュータ関連書籍＋平石の一言.pdf）